Exam Board:
OCR A-Level
Specification:
Computer Science H446
4.3 - Boolean Algebra
Watch on YouTube:
Boolean Logic (NOT, AND, OR, XOR)
Karnaugh maps
Boolean algebra rules
Logic gate diagrams
Truth tables
D-type flip flops
Half & full adders
This topic explores how the logical operations NOT, AND, OR and XOR are used to process binary data and control digital systems. It also looks at how to simplify and represent logic using Karnaugh maps, Boolean algebra rules, logic gate diagrams and truth tables.
Boolean Logic

Boolean logic is a form of algebra in which all values are either True (1) or False (0). It’s used in computing and digital circuits to make decisions and control the flow of programs.
-
NOT (negation) (¬) reverses the input value - 1 becomes 0 and 0 becomes 1.
-
AND (conjunction) (∧) outputs 1 only if both inputs are 1 (e.g. 1 AND 1 = 1, otherwise 0).
-
OR (disjunction) (v) outputs 1 if at least one input is 1 (e.g. 1 OR 0 = 1).
-
XOR (exclusive disjunction) (v) outputs 1 only if one input is 1 but not both (e.g. 1 XOR 1 = 0, 1 XOR 0 = 1).
Karnaugh Maps
A Karnaugh map is a visual method used to simplify Boolean expressions and make logic circuits more efficient. It organises all possible input combinations into a grid, where adjacent cells differ by only one bit (following Gray code order).
By grouping together 1s (representing True outputs) in powers of two (1, 2, 4 or 8 cells), you can identify and remove redundant terms in a Boolean expression. The simplified result reduces the number of logic gates needed in a circuit, making it faster and easier to build.

Boolean Algebra Rules
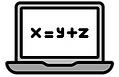
Boolean algebra rules are used to simplify Boolean expressions.
-
De Morgan’s Laws show how to distribute negation across AND and OR operations: ¬(A AND B) = (¬A OR ¬B) and ¬(A OR B) = (¬A AND ¬B).
-
Distributive Law allows expressions to be expanded or factored, e.g., A AND (B OR C) = (A AND B) OR (A AND C) and vice versa for OR over AND.
-
Associative Law means the grouping of terms doesn’t affect the result. (A AND B) AND C = A AND (B AND C) and (A OR B) OR C = A OR (B OR C).
-
Commutative Law means the order of terms doesn’t matter in Boolean operations, e.g., A AND B = B AND A and A OR B = B OR A.
- With Double Negation, two NOTs cancel each other out, returning the original value, e.g., ¬¬A = A.
Logic Gate Diagrams
Logic gate diagrams are visual representations of Boolean expressions or digital circuits, showing how data flows through logic gates to produce an output. Each gate performs a basic logical operation (such as NOT, AND, OR or XOR) and is represented by a distinct symbol.

NOT

AND

OR

XOR
Truth Tables

A truth table is used to show all possible input combinations for a logic circuit or Boolean expression, along with the resulting output for each combination.
Each row in the table represents a unique set of input values (usually 0 for False and 1 for True). The final column shows the output produced by applying the logical operations to those inputs.
The number of rows in a truth table doubles with each additional input, e.g. 4 rows for 2 inputs and 8 rows for 3 inputs.
D-Type Flip Flops
A D-type flip-flop is a sequential logic circuit that stores a single bit of data - either 0 or 1. It has two inputs, D (data) and CLK (clock), and two outputs, Q and ¬Q.
When a clock pulse occurs, the flip-flop copies the value of D to the Q output, and that value is held (stored) until the next clock pulse. This makes D-type flip-flops useful for memory storage, registers and data synchronisation.
Essentially, they act as a 1-bit memory cell, storing the last value of D whenever the clock signal triggers.
Half Adders & Full Adders
A half adder is a logic circuit with two inputs (A and B) that are added to produce two outputs - S (sum), the result of A XOR B - and C (carry), the result of A AND B. Half adders can only add two bits and cannot handle an input carry from a previous addition.
A full adder is an extension of a half adder with three inputs: A, B, and C in (a carry-in from a previous calculation). It produces two outputs: S (sum) (A XOR B XOR Cin) and C out (carry out) ((A AND B) OR (B AND Cin) OR (A AND Cin)). Full adders can be linked together to perform multi-bit binary addition in arithmetic circuits.

Questo's Key Terms
Boolean Logic: NOT, AND, OR, XOR, Karnaugh maps, logic gate diagrams, truth tables
Boolean Algebra Rules: De Morgan’s Laws, distribution, association, commutation, double negation
D-Type Flip Flops: data, clock, Q, NOT Q
Adders: half adder, full adder
Did You Know?
The word 'Boolean' is always spelt with a capital B because it is named after George Boole, a 19th-century English mathematician. His work has become the foundation of all modern digital electronics and computing.

