4.2: Signed Binary
Exam Board:
Eduqas / WJEC
Specification:
2020 +
What are Sign and Magnitude and Two's Complement?
Sign and Magnitude and Two's Complement are both methods of writing positive and negative binary values.
Sign and Magnitude is simpler but will cause incorrect answers if used in binary calculations.
Two's Complement is more complex but will generate correct answers when used in binary calculations.
Sign & Magnitude
The most significant bit (MSB) is the largest bit of a binary number - the one furthest to the left.
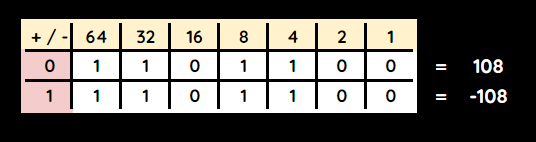
The MSB is the sign - it represents whether the binary value is positive or negative.
If the sign is 0 then the binary number is positive.
If the sign is 1 then the binary number is negative.
The other bits represent the magnitude - the value of the binary number.
For an 8-bit binary number, the range is -127 to 127, because only 7 bits are used to define the magnitude.
Sign & Magnitude: Problems
Sign and magnitude is not commonly used by computers for two main reasons:
Performing binary addition and subtraction (see section 4.3) will often cause a wrong result.
In the example below, -7 + 3 should equal -4 but the result given is 2.
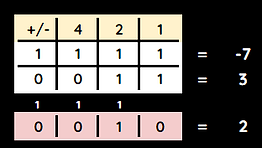
+
Sign and magnitude creates two different values for 0 - positive 0 and negative 0 which is incorrect.

Two's Complement
Two's complement is a method of representing positive and negative binary values.
It is used often by computers because binary calculations will work correctly and there is only one value for zero.
Two's Complement: Denary to Binary
To represent a negative value using two's complement follow these steps:
-
Write out the positive value in binary.
-
Start on the right-hand side and move along, copy all 0s until you get to the first 1. The first 1 is copied too.
-
After the first 1 invert each value (change to its opposite). So 0 becomes 1 and 1 becomes 0.
1.

2.

3.

Two's Complement: Binary to Denary
To convert a binary number to denary using two's complement you must remember that the MSB is a negative value.
Just add the numbers with 1 together to work out the denary value.

Questo's Questions
4.2 - Signed Binary:
Sign & Magnitude
1. Using sign and magnitude, convert the following values to denary:
-
a. 00011101
-
b. 11100011
-
c. 10110110
-
d. 01001111 [1 each]
2. Using sign and magnitude, convert the following values to binary:
-
a. 83
-
b. -13
-
c. -102
-
d. -24 [1 each]
3. Describe two problems when using sign and magnitude. [4]
4. Using sign and magnitude, the range of numbers that can be represented in 6 bits is from - 31 to + 31. State the range of numbers that can be represented using sign and magnitude in the following bits:
-
a. 8 bits
-
b. 4 bits [1 each]
Two's Complement
1. Using two's complement, convert the following values to binary:
-
a. -20
-
b. -49
-
c. -87
-
d. -113 [2 each]
2. Using two's complement, convert the following values to denary:
-
a. 10110010
-
b. 11101110
-
c. 01101011
-
d. 10011111 [2 each]
Watch the video to learn how sign and magnitude is used to represent negative numbers in binary.
Watch the video to learn how two's complement is used to represent negative numbers in binary.
Watch on YouTube
Watch on YouTube